Written by pooh at 2024/08/25

前言

前面先講一些廢話，就這大概是我從 2024 的 5 月底開始研究的一個東西，大概實際雛形完整是在 6 月中的時候，原本是想說當作我的資訊專題，但去找了蔡孟宗教授 orz 後跟他談了一下，覺得他講得挺有道理的，就這個內容大概只能當篇還不錯的 codeforces blog 或比較笨的人寫的国家集训队 20XX 论文集這種東西，所以我後來就又去做其他比較有趣一點的東西了。

然後因為前幾天發現天哪暑假要結束了，專題、資讀、免修考、校內賽等等好多東西要練喔，那我就來逃避事實架個 blog 吧，所以我就問餘切我 blog 第一篇要寫啥，他說某些教學文，但我會的而且沒有其他比較好的教學文的就只有樹分塊了QAQ，所以就有了這一篇。

最後是因為這是我第一次寫這種很多內容的文章，所以如果有看不懂的或我寫很爛的都可以來嗆我沒關係，我會盡量改。

樹分塊

好欸! 那首先先釐清一下我想要幹嘛，就那個時候我在準備資讀的分塊講義，(~~我以後不知道要怎麼水文章數的時候就會開始搬我自己做的講義過來~~)，那我當然就去研究了所謂「真‧樹上莫隊」，跟稍微看了一下樹分塊，這個時候就看到了OI wiki，然後就看到他說

OI wiki hoolan

然後我就發現，他根本在唬爛我，明明就是可以做複雜度有保證的，所以我先在這邊講一下那題在幹嘛。

Gty 的妹子树

題目大意是 : 給一棵個點的帶點權的定根樹，要求在線支援筆操作

給，將點的權改成
給，加一個編號是現在樹的大小 + 1 的點，把他的父節點當，點權設為
給，詢問點的子樹內有幾個點的點權嚴格大於

這就是我們目標要做的問題了，哪接著我們一步一步來看看要怎麼沒用快讀快寫成為這一題的最優解，然後去題解區看別人唬爛，然後再用這個樹分塊去嗆人或被嗆。

0. 小觀察跟看一下別人在幹嘛

面對這樣的一個分塊演算法，我們很直覺會希望說如果我們能有一種保證塊樹，每塊大小和連通性都很好的分塊法，可是我們先看一下樹上莫隊的那種分塊法(a.k.a. 王室分塊)，他不保證連通性欸，然後我們就跑去翻国家集训队2015论文集看鄒逍遙那一篇，然後發現他是巨砲，教你深度分塊，保證到根上的經過的數量，但不保證總數，然後你又看到有人做BFS分塊，也是一樣的狀況，甚至還有人直接用 euler tour 亂分。

反正沒有 OIer 做我們想要的，所以我們就自己做吧! ¹

1. 先定義一下

首先先謝謝 owoovo orz 在定義與證明上的幫助 ²

我們先定義比Ina弱一點但還蠻好的邊分塊(簡稱好-分塊)。 ³

Definition 1.1 : 好-分塊

當一棵樹的 (邊集) 的分割 (Partition) ，滿足

$是連通的$

為一組好-分塊

每個塊中有出現的點集為

同時定義定根樹上的好-分塊

Definition 1.2 : 好-分塊 (定根樹)

我們先將這棵定根樹的每個邊定向，方向為深度淺的節點向深度深的節點。
當一棵定根樹定向後的的分割，滿足

可以只透過內的邊到達所有內的點

為一組好-分塊

以下我們稱為”一塊”

Lemma 1.1 :

對於一組好-分塊，每一塊是一棵樹
proof :
我們先證明每一塊中任兩點簡單路徑唯一 :
假設存在之間兩條相異簡單路徑，因為，所以在原本的圖上也存在此兩條相異簡單路徑，但原圖是樹，所以矛盾。
所以每一塊有任兩點簡單路徑唯一且連通，也就是每一塊都是一棵樹

Definition 1.3 : cut

對於一組好分塊的點集，定義若一個點滿足

是這組好-分塊的一個 cut

注意到一個 cut 可能會同時出現在很多個內

Lemma 1.2 :

對於一棵定根樹的好-分塊，每個 cut 都在至少一塊中當根
proof :
WLOG 只討論一個 cut
首先我們知道與與相鄰的點只有一個深度比他淺 (樹的性質)，因此對於只有一條邊定向後是入邊，只有在存在的那一塊可能不是根，根據 cut 的定義他至少存在於至少兩塊，因此他至少會在一塊中當根。

在中當根的 cut 我稱之為 root cut

因此我們知道

Property 1.1 :

⁴

在此我 claim 說只要我們會做好-分塊，對於可於好的複雜度合併結果的詢問，我們有一個很好可以維護詢問路徑、詢問子樹、點/邊改值，加點的甚至某些情況的斷邊刪邊資料結構(?)

同時我 claim 說這個資結搬到水母圖上也可以維護詢問路徑、點 / 邊改值、加點的資料結構

痾好欸，打完嘴砲了，開始講演算法。

2. Pooh 受到 Ina 感召的樹分塊演算法 (以下簡稱樹分塊)

痾演算法的本質就是我要分塊，然後維護分塊的東西跟分塊的過程跟蓋圓方樹還有做 Tarjan 縮 BCC 很像，為了實作方便我們先定一個虛根 (因為這個符號長得很帥) ，對於一棵定根樹，我們建一條便從到根，對於不定根樹我們就任意挑一個點當根接到上⁵。

整個樹分塊分為兩部分，我稱之為 decompose
跟 build， decompose 是用一次 dfs 決定出一組好-分塊，build 是用一次 dfs 維護好每一塊的內容物與塊之間的關係。

Algorithm 2.1 decompose (定根樹)

輸入 :
一棵定根樹與
輸出 :
給你樹的一個-分塊總共有幾塊，每一個非 cut 所屬塊的編號, 每個點是否是 cut 與每一塊的 root cut

Pseudocode:

SET_BLOCK(v):
BLK_CNT++
WHILE top of DFS_STK != v do
    BLK_NUM[top of DFS_STK] := BLK_CNT
    POP DFS_STK
ENDWHILE
IS_CUT[v] := true, ROOT_CUT[BLK_CNT] := v


DFS_DECOMPOSE(v):
UNDETERMINED := 0
DFS_STK.push(v)
FOR each child u of v do
    UNDETERMINED += DFS_DECOMPOSE(u)
    IF UNDETERMINED >= K then 
        SET_BLOCK(v)
        UNDETERMINED := 0
    ENDIF
ENDFOR
RETURN UNDETERMINED

algorithm decompose():
FOR v in V do
    BLK_NUM[v] := 0, IS_CUT[v] := false
ENDFOR
BLK_CNT := 0, DFS_STK := empty_stack
FOR i = 1 to n(E)/K do
    ROOT_CUT[i] := 0
ENDFOR
ADD (0, root) to E
DFS_DECOMPOSE(0)
SET_BLOCK(0)   
RETURN BLK_CNT, BLK_NUM, IS_CUT, ROOT_CUT

Corollary 2.1 :

呼叫 decompose 的時間複雜度為
proof :
只有一次 dfs

Lemma 2.1 :

上面的演算法每一塊
proof :
我先證明，再證明

首先說明每次呼叫 , 最終的即為中有幾個元素在上 (stack 的靠近 top 的那個方向) :

考慮在沒有呼叫的狀況下顯然成立，因為即為的子樹大小，而在回傳時 dfs 序比後面的也只有的子孫。
接著說明呼叫不影響此結論，每次呼叫後會將他在上面所有元素移出，並將歸零，因此不影響此結論。

所以可以知道每一塊的該次呼叫時的 (所有且只有與在上面的屬於 )，而 (Lemma 1.1)，所以我有。

而我們對於所有，去證明他的，我們知道每次回傳值 (因為最終的)，而每一次呼叫時最大的，所以呼叫完的

總和上述兩點可證

Lemma 2.2 :

proof :
顯然 = 被呼叫的次數，可以知道在的過程中一定最少要有個點進去才會呼叫一次，加上最後呼叫的一次，總共必定少於，所以有

Lemma 2.3 :

呼叫後分出的每一塊都是連通的
proof :
每次呼叫時分到一塊的一定遞迴要回傳時在他後面的，也就是他的子樹，因此如果他在子樹內沒有呼叫到便顯然成立。而當在子樹內有呼叫到時被拔除的邊也是完整的一棵子樹，一棵樹去掉一棵子樹後還是連通，因此可以得證。

有趣的是，我們到這一步以後我們就可以發現我們做出的是一個 min-max ratio 3 以內的 CEP tree 欸，好吧可能不是很有趣，因為這個其實大家都會做。

因此根據 Lemma 2.1, Lemma 2.2, Lemma 2.3，我們可以得到的結果滿足

可以只透過內的邊到達所有內的點 (Lemma 2.3)
(Lemma 2.1)
(Lemma 2.2)

因此有

Corollary 2.2 :

後得到的分塊是一組好-分塊

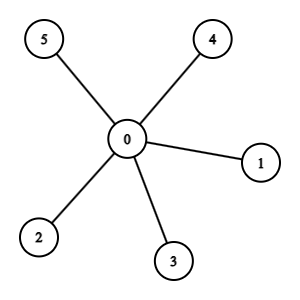
這時我們觀察到若直接用原圖，則要在塊內 dfs 時可能可能會在星狀圖 (star) 上退化到 (因為要判斷相鄰兩點是否在同一塊，會檢查所有相鄰的點)，因此需要 build 來將原圖拆成每塊獨立的森林⁶。

更明確的說，在這張圖 (Star-5) 上，當要對所屬的那一塊做事時，就會需要遍歷所有的邊，然後就死掉了，因此會需要 build。

Star_5

而因為 cut 會出現超過一次，因此我把 root cut 改建虛點，以下稱第塊的虛點編號為

Algorithm 2.2 : build

輸入 : decompose 後的所有輸出
輸出 : 一個森林代表分塊後各塊獨立的結果，代表將每塊縮成一條邊的樹。

Psuedocode :

DFS_BUILD(v):
FOR each child u of v do
    DFS_BUILD(u)
    IF BLK_NUM[v] = BLK_NUM[u] then
        ADD (v, u) to BLK_TREE
    ELSE IF IS_CUT[v] then
        ADD (vir(BLK_NUM[u]), u) to BLK_TREE
        ADD (BLK_NUM[v], BLK_NUM[u]) to CUT_TREE
    ENDIF
ENDFOR

algorithm build():
DFS_BUILD(0)
UNIQUE CUT_TREE

這裡需要 unique 的原因是因為在 star 上很有可能會有一個 block 跟他的 root 在 build 的時候建很多條邊，就會爛掉，也就是上面的註解6。

Lemma 2.4 :

對邊集的時間複雜度為
proof :
首先我們先說明總共在呼叫完後大小為，對於呼叫一次時大小最多增加 1，因此顯然成立。
接著要證這時對於每個點，邊集加入的順序一定是順序的，這一點也顯然，因為兩次 dfs 的順序相同，因此邊集的時間複雜度為

Corollary 2.3 :

呼叫的時間複雜度為

Corollary 2.4 :

呼叫 + 總空間複雜度為

比較有趣一點點的東西就講完了，實作的 code 後面會有。

3. 對於樹形固定的樹支援點改值 / 子樹詢問

我們先考慮下列問題⁷⁸

給定一棵定根樹，樹上每個點有一個權值，要求在線支援

把一個點的改掉

詢問對於給定的 , 的子樹有幾個節點滿足

這時我們可以考慮對於每一塊維護排序好的，便對於每一塊，我們可以尋問這一塊有幾個滿足，因此我們可以知道對於每一個詢問，我們可以把它拆成許多塊整塊的詢問與幾次塊內的子樹詢問。

Lemma 3.1 :

塊內的子樹詢問只會出現一次
proof :
如Lemma 2.3 中提到的，每一塊都是完整的子樹，因此將一棵樹拔掉一些完整的子樹後還是一棵樹，這棵樹必與原本的根在同一塊內，否則就不連通了，因此塊內子樹詢問只會出現一次。

因此令整塊詢問的複雜度為，塊內詢問的複雜度為，合併詢問的複雜度為，有

Corollary 3.1 :

詢問的複雜度為

而對於修改就改掉該塊維護的值就好，最糟也可以直接重蓋。
因此令修改複雜度為 , 初始維護各塊的值複雜度為，我們有

Corollary 3.2 :

總複雜度為

對於上面那一題，我們可以在每一塊維護一棵自平衡二元樹或直接維護一個 sort 好的 vector，便可分析複雜度。

Lemma 3.2 :

對於塊內維護自平衡二元樹，總操作複雜度為
proof :
套用上面的複雜度分析，， (自平衡二元樹上 insert & erase)， (自平衡二元樹上 distance)， (樹上 dfs)，，可得總複雜度為
當，時可得

Lemma 3.3 :

直接用 vector 維護排序好的點值，總操作複雜度為
套用上面的複雜度分析，， (vector insert & erase)， (vector 上二分搜)， (樹上 dfs)，，可得總複雜度為
當，時可得

兩種維護方法的複雜度是相同的，下面是三個操作的實際狀況:

Algorithm 3.1 : initialize_block

輸入 : build 後的結果
輸出 : 對於各塊維護所需的值

pseudocode :

UPDATE_VALUE(v):
INSERT VAL[v] into BLK_VALUE[BLK_NUM[v]]
FOR each child u of v in BLK_TREE do
    UPDATE_VALUE(u)
ENDFOR

algorithm initialize_block():
FOR i = 1 to BLK_CNT do 
    UPDATE_VALUE(vir(i))
ENDFOR

Algorithm 3.2 : modify

輸入 : initialize_block 後的結果，要修改的位置與修改的值
輸出 : 修改後的結果

pseudocode :

algorithm modify(v, x):
ERASE VAL[v] from BLK_VALUE[BLK_NUM[v]]
VAL[v] := x
INSERT VAL[v] into BLK_VALUE[BLK_NUM[v]]

Algorithm 3.3 : query_subtree

輸入 : initialize_block 後的結果，詢問的位置與詢問的值
輸出 : 對於該詢問的答案

pseudocode :

QEURY_BETWEEN_BLK(b, l, r):
RETURN_VAL := QUERY l, r in BLK_VALUE[b]
FOR each child u of b in CUT_TREE do
    RETURN_VAL += QUERY_BETWEEN_BLK(u, l, r)
ENDFOR
RETURN RETURN_VAL

algorithm query_subtree(v, l, r):
ANSWER := CHECK l, r with VAL[v]
FOR each u is child of v in BLK_TREE do
    ANSWER += query_subtree(u, l, r)
ENDFOR
IF IS_CUT[v] THEN
    FOR each block b with v as root cut do
        ANSWER += QUERY_BETWEEN_BLK(b, l, r)
    ENDFOR
ENDIF
RETURN ANSWER

附上cpp實作:

cpp code

待補，因為資讀好忙，你想要看的話去 part 5 啦。

4. 對於樹形固定的樹支援點(邊)改值 / 路徑詢問

我們考慮下列問題⁹¹⁰

給定一顆樹與樹上的邊權，要求在線支援

修改一條邊的邊權

詢問到的距離

我們可以發現在定根之後，我們可以把一段路徑分成幾條從塊內的某個點到 root cut 的路徑 + 幾條塊內兩非 root cut 點的路徑。

Lemma 4.1 :

一條路徑上最多只有一條兩端非 root cut 的路徑
proof : 首先對於如果 , 其中是的祖先，則可以套用 Lemma 3.1 的證明很容易的說明兩端非　root cut 的路徑是的塊內的，因次我們可以把任何到的詢問拆成到跟到，兩端非 root cut 的路徑是的塊內的。

因此我們只要在每一塊內維護從 root cut 到該節點的訊息就好了，我們便知道整體的複雜度分析就如子樹詢問的一樣。

Lemma 4.2 :

使用上面的作法總複雜度為
套用上面的複雜度分析，， (dfs 一次)， (陣列查詢一次)， (樹上 dfs)，，可得總複雜度為
當，時可得

下面是操作的實際狀況

Algorithm 4.1 : initialize block / modify

輸入 : build 後的結果 & 要修改的邊與邊權
輸出 : 各塊的維護值

pseudocode :

UPDATE_VALUE(v, distance):
TO_ROOT[v] := distance
FOR each child u of v in BLK_TREE do
    UPDATE_VALUE(u, distance + EDGE(v, u))
ENDFOR

algorithm initialize_block():
FOR i = 1 to BLK_CNT do 
    UPDATE_VALUE(vir(i), 0)
ENDFOR

algorithm modify(u, v, x):
EDGE(u, v) := x
MIN_BLOCK := min(BLK_NUM[u], BLK_NUM[v])
UPDATE_VALUE(vir(MIN_BLK), 0)

Algorithm 4.2 query :

輸入 : 詢問的路徑的兩端
輸出 : 路徑長

pseudocode :

QUERY_IN_BLOCK(u, v):
GET PATH(u, v) // by dfs or any O(K) method
LENGTH := 0
FOR each edge i on PATH(u, v) do:
    ADD WEIGHT of i to LENGTH
ENDFOR
RETURN LENGTH

algorithm query(u, v):
GET LCA(u, v) on CUT_TREE // by precomputation or any O(|V|/K) method
LCA := LCA(u, v) on CUT_TREE
LENGTH := 0
WHILE BLK_NUM[u] is not LCA do
    ADD TO_ROOT[u] to LENGTH
    u := ROOT_CUT[blk_num[u]]
ENDWHILE
WHILE BLK_NUM[v] is not LCA do
    ADD TO_ROOT[v] to LENGTH
    v := ROOT_CUT[blk_num[v]]
ENDWHILE
ADD QUERY_IN_BLOCK(u, v) to LENGTH
RETURN LENGTH

cpp實作:

cpp code

#pragma GCC optimize("O3,unroll-loops")
#pragma GCC target("avx2,bmi,bmi2,lzcnt,popcnt")
#include <bits/stdc++.h>
#define uwu return 0;

using namespace std;

const int SIZE = 2e5 + 5, K = 1e2, MAX_BLK = SIZE / K + 5;

int N;

vector<pair<int, int>> original_tree[SIZE], blk_tree[SIZE + MAX_BLK], cut_tree[MAX_BLK];

int blk_cnt = 0;

long long cost[SIZE], to_root[SIZE + MAX_BLK];

int blk_num[SIZE], root_cut[MAX_BLK];

bitset <SIZE> is_cut;

pair <int, int> edge[SIZE];

pair<int, int> cut_path[MAX_BLK][MAX_BLK];

#define fs first
#define sc second

vector<int> dfs_stk;

int dfs_decompose(int nd, int rt){
    int ret = 0;
    dfs_stk.push_back(nd);
    for(auto i:original_tree[nd]){
        if(i.fs != rt){
            ret += dfs_decompose(i.fs, nd);
            if(ret >= K){
                is_cut[nd] = 1;
                blk_cnt++;
                while(dfs_stk.back() != nd){
                    blk_num[dfs_stk.back()] = blk_cnt;
                    dfs_stk.pop_back();
                }
                root_cut[blk_cnt] = nd;
                ret = 0;
            }
        }
    }
    return ret + 1;
}

void decompose(){
    dfs_decompose(1, 0);
    is_cut[1] = 1;
    if((int)dfs_stk.size() > 1){
        blk_cnt++;
        while(dfs_stk.back() != 1){
            blk_num[dfs_stk.back()] = blk_cnt;
            dfs_stk.pop_back();
        }
        root_cut[blk_cnt] = 1;
    }
    blk_cnt++;
    blk_num[1] = blk_cnt;
    return;
}

void build_tree(int nd, int rt){
    for(auto i:original_tree[nd]){
        if(i.fs != rt){
            build_tree(i.fs, nd);
            if(blk_num[nd] == blk_num[i.fs]){
                blk_tree[nd].push_back(i);
                blk_tree[i.fs].push_back({nd, i.sc});
                continue;
            }
            if(is_cut[nd]){
                cut_tree[blk_num[nd]].push_back({blk_num[i.fs], 1});
                cut_tree[blk_num[i.fs]].push_back({blk_num[nd], 0});
                blk_tree[blk_num[i.fs] + N].push_back(i);
                blk_tree[i.fs].push_back({blk_num[i.fs] + N, i.sc});
            }
        }
    }
}

void update_blk_dis(int nd, int rt, long long dis){
    to_root[nd] = dis;
    for(auto i:blk_tree[nd]){
        if(i.fs != rt){
            update_blk_dis(i.fs, nd, cost[i.sc] + dis);
        }
    }
    return;
}

void dfs_between_blk(int nd, int rt, const int st, pair <int, int> du){
    cut_path[st][nd] = du;
    for(auto i:cut_tree[nd]){
        if(i.fs != rt){
            i.sc ? du.fs++ : du.sc++;
            dfs_between_blk(i.fs, nd, st, du);
            i.sc ? du.fs-- : du.sc--;
        }
    }
    return;
}

void build(){
    build_tree(1, 0);
    for (int i = 1; i <= blk_cnt; i++){
        sort(cut_tree[i].begin(), cut_tree[i].end());
        auto it = unique(cut_tree[i].begin(), cut_tree[i].end());
        cut_tree[i].erase(it, cut_tree[i].end());
        update_blk_dis(i + N, 0, 0LL);
    }
    for (int i = 1; i <= blk_cnt; i++){
        dfs_between_blk(i, 0, i, {0, 0});
    }
    return;
}

bool dfs_in_blk(int nd, int rt, const int tar, long long &dis){
    if(nd == tar)
        return 1;
    for(auto i:blk_tree[nd]){
        if(i.fs != rt){
            dis += cost[i.sc];
            if(dfs_in_blk(i.fs, nd, tar, dis))
                return 1;
            dis -= cost[i.sc];
        }
    }
    return 0;
}

long long query(int u, int v){
    long long dis = 0;
    pair<int, int> du = cut_path[blk_num[u]][blk_num[v]];
    while(du.fs--){
        dis += to_root[v];
        v = root_cut[blk_num[v]];
    }
    while(du.sc--){
        dis += to_root[u];
        u = root_cut[blk_num[u]];
    }
    dfs_in_blk(u, 0, v, dis);
    return dis;
}

int main(){
    cin.tie(0), ios::sync_with_stdio(0);
    cin >> N;
    for (int u, v, w, i = 1; i < N; i++){
        cin >> u >> v >> w;
        original_tree[u].push_back({v, i});
        original_tree[v].push_back({u, i});
        cost[i] = w;
        edge[i] = {u, v};
    }

    decompose();

    build();

    int Q;
    cin >> Q;

    for (int a, u, v; Q--;){
        cin >> a >> u >> v;
        if(a == 1){
            cost[u] = v;
            update_blk_dis(min(blk_num[edge[u].fs], blk_num[edge[u].sc]) + N, 0, 0LL);
        }
        if(a == 2){
            cout << query(u, v) << '\n';
        }
    }
}

5. 樹形改變 - 加點

我們考慮GTY ¹¹¹²

給定一顆定根樹，樹上每個點都有權重，要求在線支援

將點的權重改成

加上一個新的編號為點，他的父節點為，權重為

詢問對於一個節點的子樹內有多少人的權重 >

首先我們先看一些這題目前的現行解法:

1. 無複雜度保證的樹分塊

該題原本是使用一種複雜度不受保證的樹分塊做法，在星狀圖上會退化至，現存網路上主要樹分塊做法也是這種的¹³

時間: ，據說在隨機數據上是
空間:

2. 時間分塊 + 持久化線段樹

將該題轉化為壓平序上的區間小於的值的數目，便可用持久化線段樹解決，每次操作重蓋一次線段樹，每次同時要檢查這次操作對你這次詢問是否有影響，總時間複雜度為，在時可得，注意到在該題時間分塊的狀況下可以做到
(其實還可以再更優化，利用建造有序下，查詢的分塊法可以處理區間的數目，而在該題對於加點在時間分塊下維護有序的總時間是，又在時間分塊下可以用總共離散化(將 unordered_map 視為，故可以優化到時間，空間，值得注意的是該作法常數毫無人性的大，因此在實際運用上應該不適合¹⁴)
時間:
空間:

3. 塊狀鍊表

利用塊狀鍊表 + 動態祖先關係判斷可以在的時間複雜度內完成支援，取得
時間: (注意到常數會極大)
空間: (用ETT等方法支援動態祖先關係)

4. 深度 / BFS 分塊

在深度 / BFS 分塊下雖然無法確定總塊數，但可以保證到樹根上的塊數，因此可以做到在每塊支援所有子樹的點，用自平衡二元樹完成此題¹⁵
時間:
空間:

那接著看如果是我的樹分塊要怎麼做

樹分塊解

首先我們先看一個直觀的均攤想法，每個加點操作就直接將其並到原本的塊內，每
次加點操作再將整棵樹重新分塊，因此我們有所有加點操作的總時間複雜度為，而一塊的大小便為最糟，因此可以套Lemma 3.2 的複雜度分析，得到:

Lemma 5.1 :

這種樹分塊法總時間複雜度為 (在)
proof :
套用上面的複雜度分析，， (vector insert & erase)， (vector 上二分搜)， (樹上 dfs)，，可得總複雜度為
當，時可得

因此我們就做完了，好欸，但我自己在猜有可能可以證只要分的，均攤，但反正現在這樣常數很好，可以不壓常拿個落谷最佳解。

GTY_Fastest_Code

附上醜醜cpp實作

cpp code

#include <bits/stdc++.h>
#define uwu return 0;

using namespace std;

#include <bits/extc++.h>
using namespace __gnu_pbds;

const int SIZE = 6e4 + 5, K = 6e3, MAX_BLK = SIZE / K + 5, B = 1.7e4;

int N, Q;

vector <int> undirected_tree[SIZE], original_tree[SIZE], blk_tree[SIZE + MAX_BLK], cut_tree[MAX_BLK];

int blk_cnt = 0;

tree <pair<int, int>, null_type, less<pair<int, int>>, rb_tree_tag, tree_order_statistics_node_update> blk_val[MAX_BLK];
vector <int> sub_blk[SIZE];

int blk_num[SIZE + MAX_BLK], node_val[SIZE], blk_to_cut[MAX_BLK];

bitset <SIZE> is_cut;

vector <int> dfs_stk;

int dfs_decompose(int nd){
    int ret = 0;
    dfs_stk.push_back(nd);
    for(auto i:original_tree[nd]){
        ret += dfs_decompose(i);
        if(ret >= K){
            is_cut[nd] = 1;
            blk_cnt++;
            sub_blk[nd].push_back(blk_cnt);
            while(dfs_stk.back() != nd){
                blk_num[dfs_stk.back()] = blk_cnt;
                dfs_stk.pop_back();
            }
            blk_to_cut[blk_cnt] = nd;
            ret = 0;
        }
    }
    return ret + 1;
}

void decompose(){
    dfs_decompose(1);
    is_cut[1] = 1;
    if((int)dfs_stk.size() > 1){
        blk_cnt++;
        sub_blk[1].push_back(blk_cnt);
        while(dfs_stk.back() != 1){
            blk_num[dfs_stk.back()] = blk_cnt;
            dfs_stk.pop_back();
        }
        blk_to_cut[blk_cnt] = 1;
    }
    blk_cnt++;
    blk_num[1] = blk_cnt;
    return;
}

void build_tree(int nd){
    for(auto i:original_tree[nd]){
        build_tree(i);
        if(blk_num[nd] == blk_num[i]){
            blk_tree[nd].push_back(i);
            continue;
        }
        if(is_cut[nd]){
            cut_tree[blk_num[nd]].push_back(blk_num[i]);
            blk_tree[blk_num[i] + SIZE].push_back(i);
        }
    }
    return;
}

void update_blk_val(int nd){
    for(auto i:blk_tree[nd]){
        update_blk_val(i);
        blk_val[blk_num[nd]].insert({node_val[i], i});
    }
    return;
}

void build(){
    build_tree(1);
    blk_val[blk_cnt].insert({node_val[1], 1});
    for (int i = 1; i <= blk_cnt; i++){
        auto it = unique(cut_tree[i].begin(), cut_tree[i].end());
        cut_tree[i].erase(it, cut_tree[i].end());
        blk_num[i + SIZE] = i;
        update_blk_val(i + SIZE);
    }
    return;
}

void clear_tree(){
    for (int i = 1; i <= blk_cnt; i++){
        cut_tree[i].clear();
        blk_val[i].clear();
        blk_to_cut[i] = 0;
        blk_tree[i + SIZE].clear();
        blk_num[i + SIZE] = 0;
    }
    for (int i = 1; i <= N; i++){
        blk_tree[i].clear();
        blk_num[i] = 0;
        sub_blk[i].clear();
    }
    is_cut.reset();
    blk_cnt = 0;
    dfs_stk.clear();
    return;
}

int dfs_between_blk(int nd, int x){
    int ret = 0;
    for(auto i:cut_tree[nd]){
        ret += dfs_between_blk(i, x);
    }
    if(blk_val[nd].upper_bound({x, SIZE}) != blk_val[nd].end())
        ret += blk_val[nd].size() -  blk_val[nd].order_of_key(*blk_val[nd].upper_bound({x, SIZE}));
    return ret;
}

int query(int nd, int x){
    int ret = 0;
    for(auto i:blk_tree[nd]){
        ret += query(i, x);
    }
    if(nd < SIZE)
        ret += node_val[nd] > x;
    if(is_cut[nd]){
        for(auto i:sub_blk[nd]){
            ret += dfs_between_blk(i, x);
        }
    }
    return ret;
}

void modify(int nd, int x){
    #define bkv blk_val[blk_num[nd]]
    if(node_val[nd] != -1){
        bkv.erase(bkv.lower_bound({node_val[nd], nd}));
    }
    node_val[nd] = x;
    bkv.insert({x, nd});
    #undef bkv
    return;
}

void add(int rt, int x){
    int nd = ++N;
    original_tree[rt].push_back(nd);
    blk_tree[rt].push_back(nd);
    blk_num[nd] = blk_num[rt];
    node_val[nd] = -1;
    modify(nd, x);
    return;
}

void direct(int nd, int rt){
    for(auto i:undirected_tree[nd]){
        if(i != rt){
            original_tree[nd].push_back(i);
            direct(i, nd);
        }
    }
    return;
}

int main(){
    cin.tie(0), ios::sync_with_stdio(0);
    cin >> N;

    for (int i = 1, u, v; i < N; i++){
        cin >> u >> v;
        undirected_tree[u].push_back(v);
        undirected_tree[v].push_back(u);
    }

    direct(1, 0);

    for (int i = 1; i <= N; i++){
        cin >> node_val[i];
    }

    cin >> Q;

    for (int op, u, x, i = 0, last = 0; i < Q; i++){
        if(i % B == 0){
            clear_tree();
            decompose();
            build();
        }
        cin >> op >> u >> x;
        u ^= last, x ^= last;
        if(op == 0){
            last = query(u, x);
            cout << last << '\n';
        }
        if(op == 1){
            modify(u, x);
        }
        if(op == 2){
            add(u, x);
        }
    }

    uwu
}

到這邊大概就堪用了，後面有一些我自己覺得可做的東西，有空再補。

6. 利用樹形結合持久化資節 (內容待補)

就都只從每個節點的父節點的版本做修改

7. 樹形改變 - 任意定根 & merge / split (內容待補)

聽 owoovo 說可能可以每塊ETT / Menghani-Matani，owoovo 巨砲

8. 水母圖上改 (內容待補)

把環縮點當根，然後就變序列 + 樹了

9. 類似虛樹的操作 (內容待補)

這題也可以做
因為我有每個點到blk_num比他小的點一定會經過blk_num比較小的人的root cut

總結

第一次寫這種東西，寫得有點爛，但反正都寫了，後面內容待補的如果你通靈出我想講啥然後幫我寫我會很感激地直接放上來，還是再感謝一次 owoovo 跟 Ina，然後我就要回去做正事了，881。

1.之所以說 OIer 是因為吳邦一老師就有寫這篇酷東西↩
2.謝謝施竣耀學長 orzorz↩
3.沒辦法，Ina 太強了↩
4.在此表示根據該分塊法下 cut 的數量↩
5.下方的pseudocode我改成用0↩
6.同時在星狀圖上，若沒有對邊集 unique，cut tree 極有可能會有條邊，也會造成時間複雜度的問題↩
7.在線版的樹學奧林匹亞 by 陳柏凱 becaido orz↩
8.這一題也有複雜度較好的解(例如樹壓平後在線段樹的每一個節點維護一棵自平衡二元樹，總時間複雜度為)， caido 是出離線的然後 cdq 他啦。↩
9.Distance Queries on a Tree from Atcoder Beginner Contest 294↩
10.此題也有複雜度較好的解法(也比較好寫)，例如HLD () 或壓平+線段樹 ()↩
11.痾就是Gty的妹子树 ↩
12.這題目前在沒有看到時間優於我的作法的，我的作法也是現在洛谷與hydro OJ 上的最佳解，下方會有相關的複雜度分析↩
13.可以見ypy的題解，有趣的是其中一些實作已經十分接近我的有複雜度保證的做法了，而且我是在想到我的作法後才發現這一篇的↩
14.實作細節見chenxinyang的題解 ↩
15.見Haishu海树的題解 ↩